We have been working on an active matter game! If you want to challenge your colleagues or family members to a game and have them learn about active matter look no further!
The active matter game has been designed over the course of the ITN as a new outreach activity that everyone can print at home. It has been rigorously tested at almost every Active Matter Meeting. It took a few revisions but we have made a fun game for all ages. You can read all about it in the supplementary info of the new Active Matter book.
The game has been developed and finalised by Alireza Khoshzaban, Carolina van Baalen, David Bronte Ciriza, Davide Breoni, Jesús Manuel Antúnez Domínguez, Laura Natali and Sandrine Heijnen.
You only have to wait until the release date till everything will be online! We can’t wait to share it with you!
Author: Davide Breoni
Patchy landscapes promote stability of small groups on arXiv
Patchy landscapes promote stability of small groups
Gianni Jacucci, Davide Breoni, Sandrine Heijnen, José Palomo, Philip Jones, Hartmut Löwen, Giorgio Volpe, Sylvain Gigan
arXiv:2310.01620
Abstract: Group formation and coordination are fundamental characteristics of living systems, essential for performing tasks and ensuring survival. Interactions between individuals play a key role in group formation, and the impact of resource distributions is a vibrant area of research. Using active particles in a tuneable optical environment as a model system, we demonstrate that heterogeneous energy source distributions result in smaller, more stable groups with reduced individual exchange between clusters compared to homogeneous conditions. Reduced group sizes can be beneficial to optimise resources in heterogeneous environments and to control information flow within populations. Devoid of biological complications, our system provides insights into the importance of patchy landscapes in ecological dynamics and holds implications for refining swarm intelligence algorithms and enhancing crowd control techniques.
Giant Activity-Induced Stress Plateau in Entangled Polymer Solutions on arXiv
Giant Activity-Induced Stress Plateau in Entangled Polymer Solutions
Davide Breoni, Christina Kurzthaler, Benno Liebchen, Hartmut Löwen, Suvendu Mandal
arXiv:2310.02929
Abstract: We study the viscoelastic properties of highly entangled, flexible, self-propelled polymers using Brownian dynamics simulations. Our results show that the active motion of the polymer increases the height of the stress plateau by orders of magnitude due to the emergence of grip forces at entanglement points. Identifying the activity-induced energy of a single polymer and the ratio of polymer length to self-propulsion velocity as relevant energy and time scales, we find the stress autocorrelation functions collapse across Péclet numbers. We predict that the long-time viscosity scales with polymer length squared ∼L^2, in contrast to equilibrium counterparts ∼L^3. These insights offer prospects for designing new materials with activity-responsive mechanical properties.
Presentation by Davide Breoni at the DPG Spring Meeting of the Condensed Matter Section in Dresden, Germany, 26th – 31st of March 2023
Davide presented his work at the 2023 DPG Spring Meeting of the Condensed Matter Section in Dresden, Germany. His presentation “Active Brownian Particles in a disordered motility environment“, focuses on the study of Janus particles in a speckle light field.
Presentation by Davide Breoni at the APS March Meeting in Las Vegas, United States, 5th – 10th of March 2023
Davide presented his work at the 2023 APS March Meeting in Las Vegas, United States. His presentation “Active Brownian Particles in a disordered motility environment“, focuses on the study of Janus particles in a speckle light field.
Interview with Davide Breoni for EPJE highlights
Davide Breoni was interviewed for an highlight article of The European Physical Journal E. The interview “Modelling the collective movement of bacteria” refers to the article “A one-dimensional three-state run-and-tumble model with a ‘cell cycle’“, published on the same EPJE issue.
A one-dimensional three-state run-and-tumble model with a ‘cell cycle’ published in EPJE
Davide Breoni, Fabian Schwarzendahl, Ralf Blossey, Hartmut Löwen
The European Physics Journal E 45, 83 (2022)
arXiv: 2206.00992
DOI:10.1140/epje/s10189-022-00238-7
We study a one-dimensional three-state run-and-tumble model motivated by the bacterium Caulobacter crescentus which displays a cell cycle between two non-proliferating mobile phases and a proliferating sedentary phase. Our model implements kinetic transitions between the two mobile and one sedentary states described in terms of their number densities, where mobility is allowed with different running speeds in forward and backward direction. We start by analyzing the stationary states of the system and compute the mean and squared-displacements for the distribution of all cells, as well as for the number density of settled cells. The latter displays a surprising super-ballistic scaling ∼t^3 at early times. Including repulsive and attractive interactions between the mobile cell populations and the settled cells, we explore the stability of the system and employ numerical methods to study structure formation in the fully nonlinear system. We find traveling waves of bacteria, whose occurrence is quantified in a non-equilibrium state diagram.
Poster by Davide at the Active Matter and Active Media Summer School 2022, Cargèse, France
Brownian particles driven by spatially periodic noise published in EPJE
Brownian particles driven by spatially periodic noise
Davide Breoni, Ralf Blossey, Hartmut Löwen
The European Physical Journal E 45, 18 (2022)
arXiv: 2111.10220
DOI:10.1140/epje/s10189-022-00176-4
We discuss the dynamics of a Brownian particle under the influence of a spatially periodic noise strength in one dimension using analytical theory and computer simulations. In the absence of a deterministic force, the Langevin equation can be integrated formally exactly. We determine the short- and long-time behaviour of the mean displacement (MD) and mean-squared displacement (MSD). In particular we find a very slow dynamics for the mean displacement, scaling as t^(-1/2) with time t. Placed under an additional external periodic force near the critical tilt value we compute the stationary current obtained from the corresponding Fokker-Planck equation and identify an essential singularity if the minimum of the noise strength is zero. Finally, in order to further elucidate the effect of the random periodic driving on the diffusion process, we introduce a phase factor in the spatial noise with respect to the external periodic force and identify the value of the phase shift for which the random force exerts its strongest effect on the long-time drift velocity and diffusion coefficient.
Active noise-driven particles under space-dependent friction in one dimension on arXiv
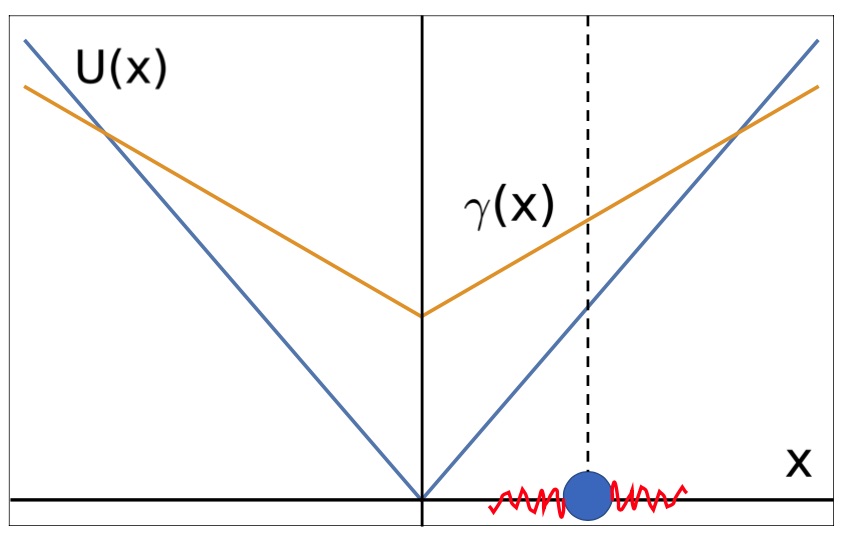
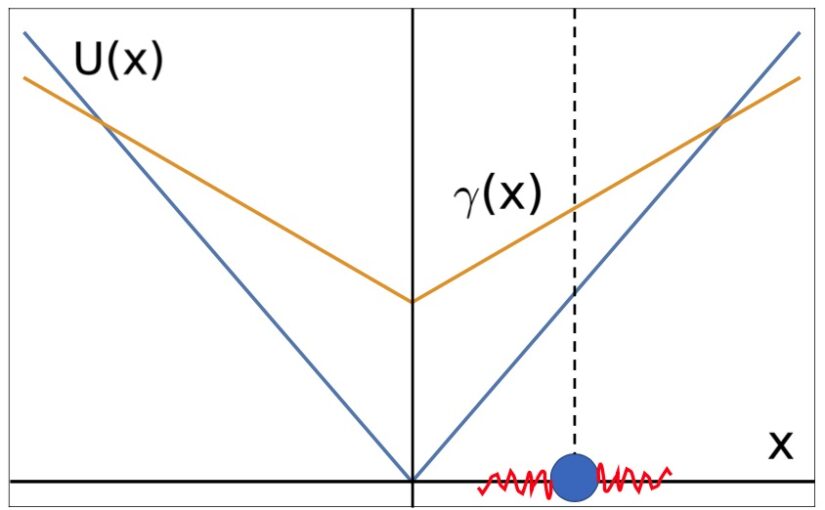
Davide Breoni, Ralf Blossey, Hartmut Löwen
arxiv: 2102.09944
Abstract: We study a Langevin equation describing the stochastic motion of a particle in one dimension with coordinate x, which is simultaneously exposed to a space-dependent friction coefficient γ (x), a confining potential U(x) and non-equilibrium (i.e., active) noise. Specically, we consider frictions γ (x) = γ0 + γ1|x|p and potentials U(x) ∝ |x|p with exponents p = 1; 2 and n = 0; 1; 2. We provide analytical and numerical results for the particle dynamics for short times and the stationary
probability density functions (PDFs) for long times. The short-time behaviour displays diffusive and ballistic regimes while the stationary PDFs display unique characteristic features depending on the exponent values (p; n). The PDFs interpolate between Laplacian, Gaussian and bimodal distributions, whereby a change between these different behaviours can be achieved by a tuning of the friction strengths ratio
γ0 / γ1. Our model is relevant for molecular motors moving on a
one-dimensional track and can also be realized for confined self-propelled colloidal particles.