Month: February 2021
Active noise-driven particles under space-dependent friction in one dimension on arXiv
Davide Breoni, Ralf Blossey, Hartmut Löwen
arxiv: 2102.09944
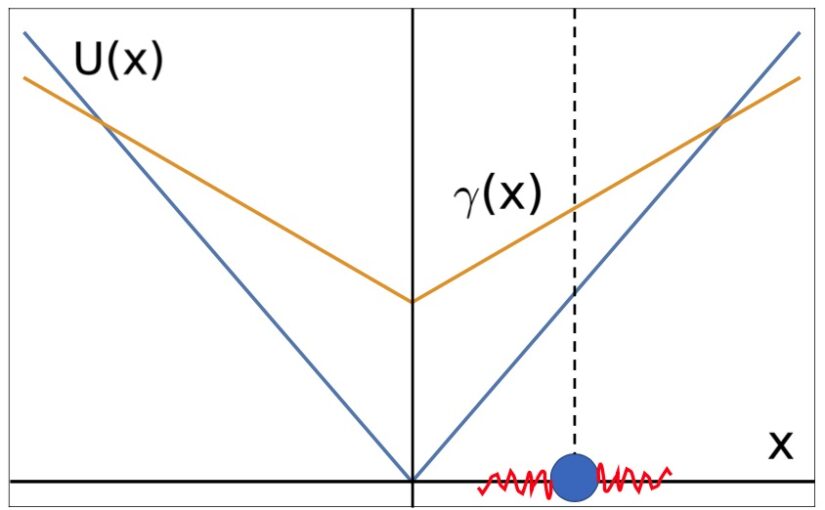
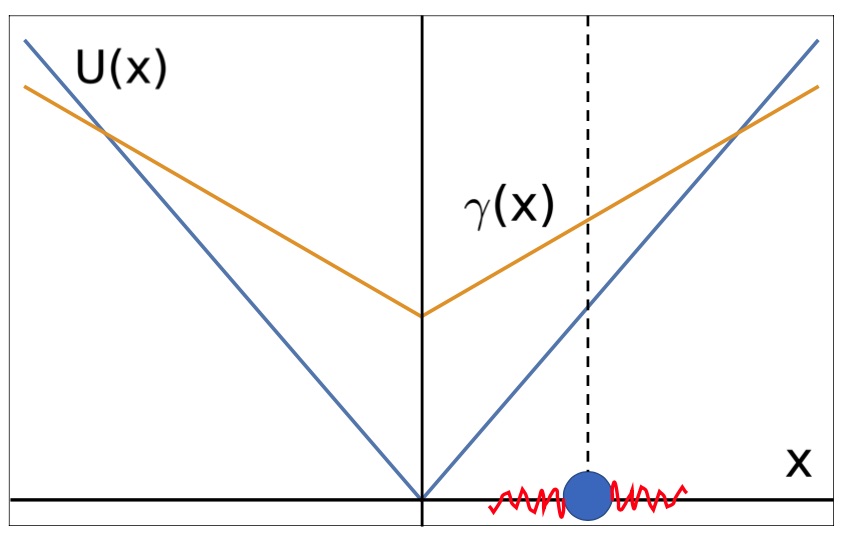
Abstract: We study a Langevin equation describing the stochastic motion of a particle in one dimension with coordinate x, which is simultaneously exposed to a space-dependent friction coefficient γ (x), a confining potential U(x) and non-equilibrium (i.e., active) noise. Specically, we consider frictions γ (x) = γ0 + γ1|x|p and potentials U(x) ∝ |x|p with exponents p = 1; 2 and n = 0; 1; 2. We provide analytical and numerical results for the particle dynamics for short times and the stationary
probability density functions (PDFs) for long times. The short-time behaviour displays diffusive and ballistic regimes while the stationary PDFs display unique characteristic features depending on the exponent values (p; n). The PDFs interpolate between Laplacian, Gaussian and bimodal distributions, whereby a change between these different behaviours can be achieved by a tuning of the friction strengths ratio
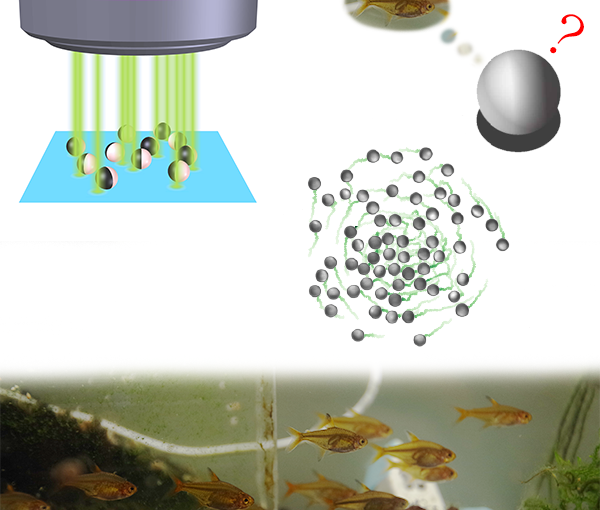
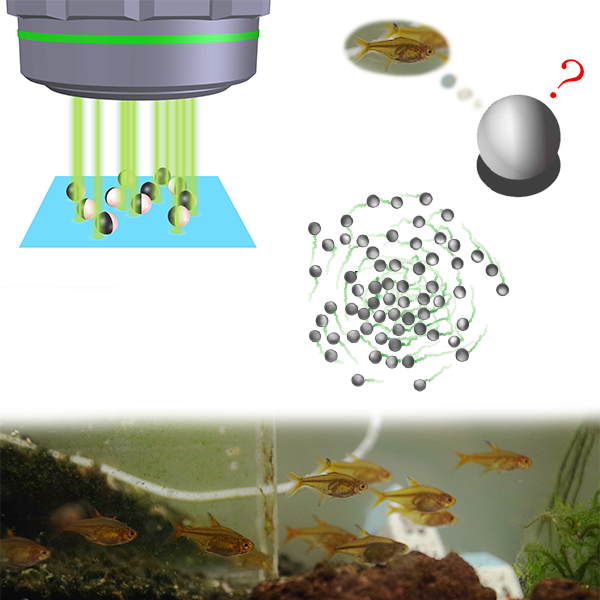
γ0 / γ1. Our model is relevant for molecular motors moving on a
one-dimensional track and can also be realized for confined self-propelled colloidal particles.