Tag: Ralf Blossey

A one-dimensional three-state run-and-tumble model with a ‘cell cycle’ published in EPJE

Graphical abstract of the publication. (Image from the article.)
A one-dimensional three-state run-and-tumble model with a ‘cell cycle’
Davide Breoni, Fabian Schwarzendahl, Ralf Blossey, Hartmut Löwen
The European Physics Journal E 45, 83 (2022)
arXiv: 2206.00992
DOI:10.1140/epje/s10189-022-00238-7

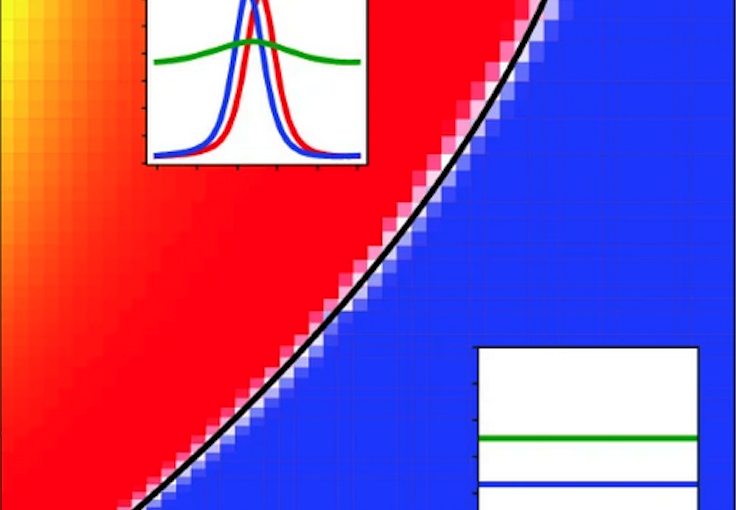
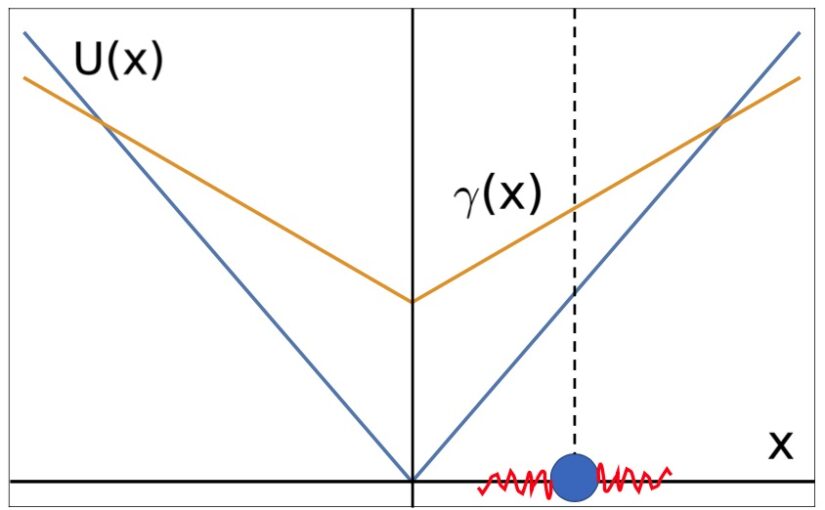
We study a one-dimensional three-state run-and-tumble model motivated by the bacterium Caulobacter crescentus which displays a cell cycle between two non-proliferating mobile phases and a proliferating sedentary phase. Our model implements kinetic transitions between the two mobile and one sedentary states described in terms of their number densities, where mobility is allowed with different running speeds in forward and backward direction. We start by analyzing the stationary states of the system and compute the mean and squared-displacements for the distribution of all cells, as well as for the number density of settled cells. The latter displays a surprising super-ballistic scaling ∼t^3 at early times. Including repulsive and attractive interactions between the mobile cell populations and the settled cells, we explore the stability of the system and employ numerical methods to study structure formation in the fully nonlinear system. We find traveling waves of bacteria, whose occurrence is quantified in a non-equilibrium state diagram.

Brownian particles driven by spatially periodic noise published in EPJE

Brownian particles driven by spatially periodic noise
Davide Breoni, Ralf Blossey, Hartmut Löwen
The European Physical Journal E 45, 18 (2022)
arXiv: 2111.10220
DOI:10.1140/epje/s10189-022-00176-4

We discuss the dynamics of a Brownian particle under the influence of a spatially periodic noise strength in one dimension using analytical theory and computer simulations. In the absence of a deterministic force, the Langevin equation can be integrated formally exactly. We determine the short- and long-time behaviour of the mean displacement (MD) and mean-squared displacement (MSD). In particular we find a very slow dynamics for the mean displacement, scaling as t^(-1/2) with time t. Placed under an additional external periodic force near the critical tilt value we compute the stationary current obtained from the corresponding Fokker-Planck equation and identify an essential singularity if the minimum of the noise strength is zero. Finally, in order to further elucidate the effect of the random periodic driving on the diffusion process, we introduce a phase factor in the spatial noise with respect to the external periodic force and identify the value of the phase shift for which the random force exerts its strongest effect on the long-time drift velocity and diffusion coefficient.

Active noise-driven particles under space-dependent friction in one dimension on arXiv

Sketch of the confining potential U(x) = κ|x|, a linear friction gradient γ(x) = γ0+γ1|x| in arbitrary units. The particle, shown by a blue dot on the x-axis, is activated by noise (indicated in red), under the influence of the potential and the friction gradient. Image by D. Breoni.
Active noise-driven particles under space-dependent friction in one dimension

Davide Breoni, Ralf Blossey, Hartmut Löwen
arxiv: 2102.09944

Abstract: We study a Langevin equation describing the stochastic motion of a particle in one dimension with coordinate x, which is simultaneously exposed to a space-dependent friction coefficient γ (x), a confining potential U(x) and non-equilibrium (i.e., active) noise. Specically, we consider frictions γ (x) = γ0 + γ1|x|p and potentials U(x) ∝ |x|p with exponents p = 1; 2 and n = 0; 1; 2. We provide analytical and numerical results for the particle dynamics for short times and the stationary
probability density functions (PDFs) for long times. The short-time behaviour displays diffusive and ballistic regimes while the stationary PDFs display unique characteristic features depending on the exponent values (p; n). The PDFs interpolate between Laplacian, Gaussian and bimodal distributions, whereby a change between these different behaviours can be achieved by a tuning of the friction strengths ratio
γ0 / γ1. Our model is relevant for molecular motors moving on a
one-dimensional track and can also be realized for confined self-propelled colloidal particles.