Davide Breoni, Fabian Schwarzendahl, Ralf Blossey, Hartmut Löwen
The European Physics Journal E 45, 83 (2022)
arXiv: 2206.00992
DOI:10.1140/epje/s10189-022-00238-7
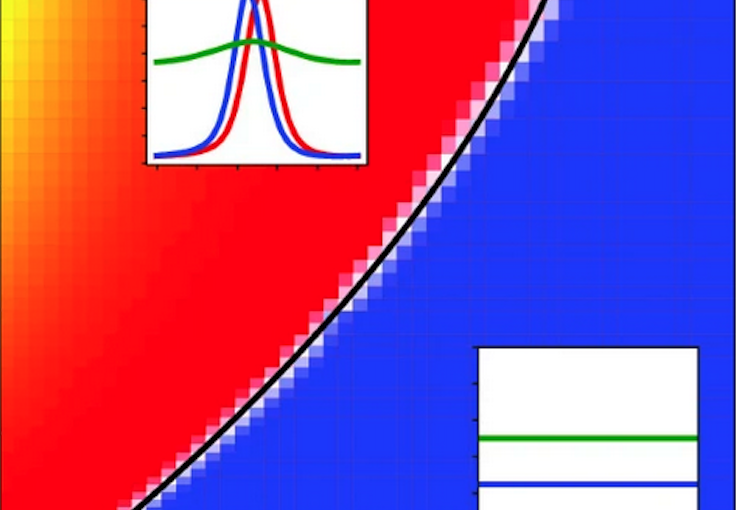
We study a one-dimensional three-state run-and-tumble model motivated by the bacterium Caulobacter crescentus which displays a cell cycle between two non-proliferating mobile phases and a proliferating sedentary phase. Our model implements kinetic transitions between the two mobile and one sedentary states described in terms of their number densities, where mobility is allowed with different running speeds in forward and backward direction. We start by analyzing the stationary states of the system and compute the mean and squared-displacements for the distribution of all cells, as well as for the number density of settled cells. The latter displays a surprising super-ballistic scaling ∼t^3 at early times. Including repulsive and attractive interactions between the mobile cell populations and the settled cells, we explore the stability of the system and employ numerical methods to study structure formation in the fully nonlinear system. We find traveling waves of bacteria, whose occurrence is quantified in a non-equilibrium state diagram.