Roadmap for optical tweezers
Giovanni Volpe, Onofrio M Maragò, Halina Rubinsztein-Dunlop, Giuseppe Pesce, Alexander B Stilgoe, Giorgio Volpe, Georgiy Tkachenko, Viet Giang Truong, Síle Nic Chormaic, Fatemeh Kalantarifard, Parviz Elahi, Mikael Käll, Agnese Callegari, Manuel I Marqués, Antonio A R Neves, Wendel L Moreira, Adriana Fontes, Carlos L Cesar, Rosalba Saija, Abir Saidi, Paul Beck, Jörg S Eismann, Peter Banzer, Thales F D Fernandes, Francesco Pedaci, Warwick P Bowen, Rahul Vaippully, Muruga Lokesh, Basudev Roy, Gregor Thalhammer-Thurner, Monika Ritsch-Marte, Laura Pérez García, Alejandro V Arzola, Isaac Pérez Castillo, Aykut Argun, Till M Muenker, Bart E Vos, Timo Betz, Ilaria Cristiani, Paolo Minzioni, Peter J Reece, Fan Wang, David McGloin, Justus C Ndukaife, Romain Quidant, Reece P Roberts, Cyril Laplane, Thomas Volz, Reuven Gordon, Dag Hanstorp, Javier Tello Marmolejo, Graham D Bruce, Kishan Dholakia, Tongcang Li, Oto Brzobohatý, Stephen H Simpson, Pavel Zemánek, Felix Ritort, Yael Roichman, Valeriia Bobkova, Raphael Wittkowski, Cornelia Denz, G V Pavan Kumar, Antonino Foti, Maria Grazia Donato, Pietro G Gucciardi, Lucia Gardini, Giulio Bianchi, Anatolii V Kashchuk, Marco Capitanio, Lynn Paterson, Philip H Jones, Kirstine Berg-Sørensen, Younes F Barooji, Lene B Oddershede, Pegah Pouladian, Daryl Preece, Caroline Beck Adiels, Anna Chiara De Luca, Alessandro Magazzù, David Bronte Ciriza, Maria Antonia Iatì, Grover A Swartzlander Jr
Journal of Physics: Photonics 2(2), 022501 (2023)
arXiv: 2206.13789
doi: 110.1088/2515-7647/acb57b
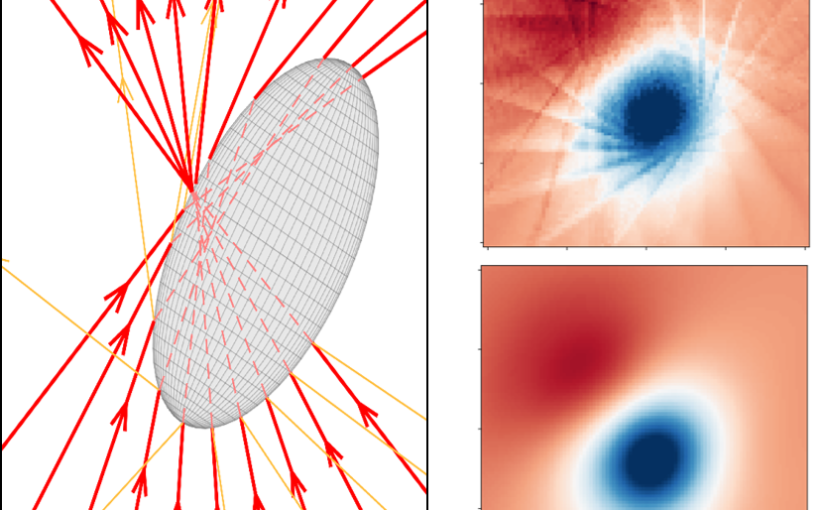
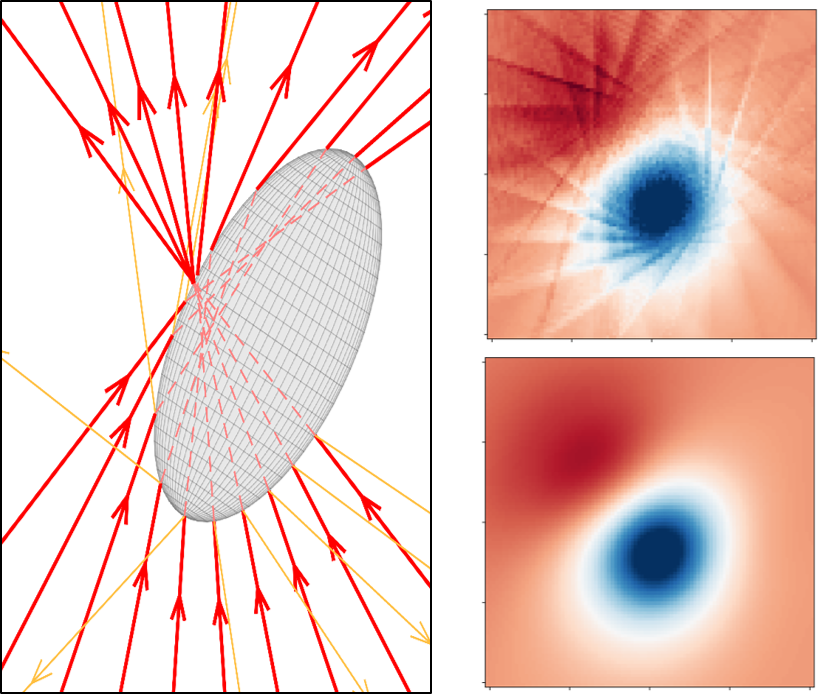
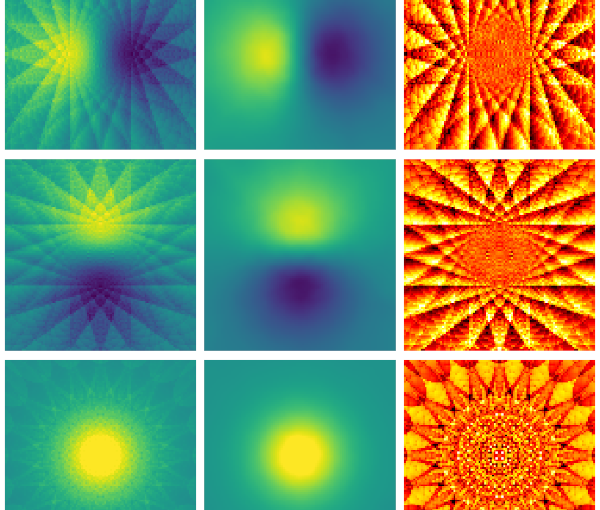
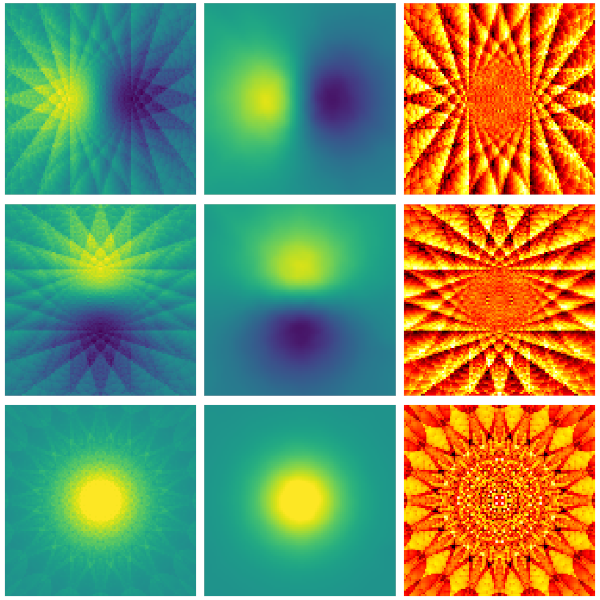
Optical tweezers are tools made of light that enable contactless pushing, trapping, and manipulation of objects, ranging from atoms to space light sails. Since the pioneering work by Arthur Ashkin in the 1970s, optical tweezers have evolved into sophisticated instruments and have been employed in a broad range of applications in the life sciences, physics, and engineering. These include accurate force and torque measurement at the femtonewton level, microrheology of complex fluids, single micro- and nano-particle spectroscopy, single-cell analysis, and statistical-physics experiments. This roadmap provides insights into current investigations involving optical forces and optical tweezers from their theoretical foundations to designs and setups. It also offers perspectives for applications to a wide range of research fields, from biophysics to space exploration.